 Sample size estimation is an important part of study planning. If the sample size is too small, the study will be underpowered, meaning it will be incapable of detecting sufficiently small differences as statistically significant. If the sample size is too large, the study will be inefficient and cost more than necessary.
Sample size estimation is an important part of study planning. If the sample size is too small, the study will be underpowered, meaning it will be incapable of detecting sufficiently small differences as statistically significant. If the sample size is too large, the study will be inefficient and cost more than necessary.A critical component of sample size estimation formulas is the standard deviation of the metric. As the standard deviation increases, so does the sample size needed to conduct a study with equivalent confidence, power, and precision.
In a series of articles, we have explored typical standard deviations for rating scales and used them to create tables that researchers can use for study planning (including side-by-side comparison with sample size estimates for binary metrics):
- How Variable Are UX Rating Scales? Data from 100,000 Responses
- The Variability and Reliability of Standardized UX Scales
- How to Estimate the Standard Deviation for Rating Scales
- Sample Sizes for Rating Scale Confidence Intervals
- Sample Sizes for Comparing Rating Scales to a Benchmark
When we started working on sample size tables for comparing two rating scale means, we noticed something strange about sample size estimates for differences in dependent proportions, which are typically assessed with the McNemar Exact Test.
In this article, we demonstrate how sample size estimation patterns for dependent proportions differ from patterns for independent proportions. We explain why this happens and suggest a strategy for building appropriate sample size tables for comparison of dependent proportions.
Sample Size Estimation Patterns for Differences in Independent and Dependent Proportions
We start with a quick recap of the experimental designs that produce independent or dependent proportions, followed by the relevant sample size estimation formulas and a series of sample size tables that demonstrate the different sample size estimation patterns.
Quick Recap of Between- and Within-Subjects Experimental Designs
The two fundamental experimental designs, using terminology from early 20th-century experimental psychology, are between-subjects and within-subjects.
Between-subjects. When the metrics from which proportions are computed come from two different groups of people, the comparison is between-subjects (independent proportions; e.g., the proportion of online banking users who are under 40 years of age and the proportion of online banking users who are 40 or older).
Within-subjects. When the same people are measured twice, the comparison is within-subjects (dependent proportions; e.g., the proportion of people who would be willing to use online banking with the proportion of the same people who would be willing to use an ATM).
Sample Size Estimation Formulas
Sample size estimation formulas can be derived from the formulas for tests of statistical significance or confidence intervals. For details on the derivation of these formulas, see Quantifying the User Experience (Sauro & Lewis, 2016).
For between-subjects studies with comparison of independent proportions, the sample size estimation formula for one independent group is:
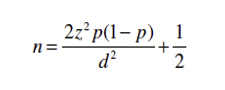
For within-subjects studies with comparison of dependent proportions, the sample size estimation formula is:
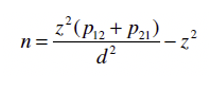
The formulas have some similarities, common with any sample size formula.
In sample size formulas, z is the symbol for the sum of two values from a standardized normal distribution: zα for the desired level of confidence and zβ for the desired level of power. Typical values for zα are 1.96 for 95% confidence (testing for p < .05) and 1.645 for 90% confidence (testing for p < .10). The most common value for zβ is 0.842 for 80% power.
Both formulas also include the symbol d, which represents the smallest unstandardized effect size (difference in proportions) that is important to identify as statistically significant.
The formulas differ in their estimates of variability, which is p(1 − p) for independent proportions and the sum of discordant proportions (p12 + p21) for dependent proportions.
When you’re not sure what the values of p will be in a between-subjects study, the typical strategy is to set p = .50. All other things being equal, this is the value at which binomial variance is maximized and p = .50 is a plausible outcome. We have seen many independent proportions that have values close to .50. Any sample size that is adequate for meeting the precision requirements of a study when p = .50 will be more than adequate when p is larger or smaller than .50.
Things get more complicated when proportions are dependent. The component (p12 + p21) in the numerator is the sum of the two types of discordant proportions that can occur in a within-subjects study. For example, Table 1 shows the counts of and nomenclature for concordant and discordant pairs for successful task completion with two designs.
| Design B Pass | Design B Fail | Total | |
|---|---|---|---|
| Design A Pass | 7 (a) | 6 (b) | 13 (m) |
| Design A Fail | 1 (c) | 1 (d) | 2 |
| Total | 8 (r) | 7 (s) | 15 (N) |
In the table, cells a (passing with both designs) and d (failing with both designs) are counts of concordant pairs. Cells b (passing with Design A and failing with Design B) and c (passing with Design B and failing with Design A) are counts of discordant pairs. Some key proportions computed from this table are:
- p1 = m/N (e.g., 13/15 = .866)
- p2 = r/N (e.g., 8/15 = .533)
- p12 = b/N (e.g., 6/15 = .400)
- p21 = c/N (e.g., 1/15 = .067)
These proportions show that the success rate for Design A was 86.6% and for Design B was 53.3%, a difference of 33.3%. The proportions for discordant pairs were 40.0% for successes with Design A and 6.7% for successes with Design B, also a difference of 33.3%. From the math used to compute these proportions, it is always true that p12 − p21 will equal p1 − p2 (which is also the definition of d).
This complication makes it difficult to recommend a default value to use for p12 + p21. Mathematically, the sum of the discordant proportions can’t exceed 1 and will equal 1 (maximum variability) only when all pairs are discordant. In our experience, an outcome this extreme is rare, so for practical UX research, we don’t recommend setting the sum of p12 + p21 to 1. Mathematically, if you set p12 = p21, then the sample size formula crashes (i.e., result is undefined) because p12 − p21 = d = 0. You can’t estimate sample sizes that can detect a 0 difference between proportions.
For practical sample size estimation when proportions are dependent, we need to understand the possible range of values for discordant proportions and, within the possible range, what values are reasonably likely.
Investigation of Typical and High Sums of Discordant Proportions
We’ve previously investigated maximum realistic variability for the Net Promoter Score trinomial and rating scale metrics, then used reasonably conservative (but less than maximum) estimates of variability to guide sample size estimation for these metrics.
In 2020, Smith and Ruxton published research on the effective use of the McNemar test. As part of that research, they collected data from 50 published real-world examples of using the McNemar Exact Test to analyze the significance of discordant proportions.
We conducted our own analysis of the data from these 50 studies to characterize the values of p1, p2, p12, and p21, as shown in Table 2.
| Analysis | p1 | p2 | p12 | p21 | Mean(p12,p21) |
|---|---|---|---|---|---|
| Max | 0.99 | 1.00 | 0.68 | 0.90 | 0.50 |
| Min | 0.09 | 0.00 | 0.00 | 0.00 | 0.01 |
| Mean | 0.46 | 0.44 | 0.24 | 0.21 | 0.22 |
| Median | 0.43 | 0.39 | 0.17 | 0.09 | 0.22 |
| 75th %ile | 0.60 | 0.63 | 0.42 | 0.35 | 0.28 |
| 25th %ile | 0.29 | 0.25 | 0.04 | 0.02 | 0.13 |
These 50 studies had a wide range of outcomes, enhancing the generalizability of our findings. The minimum and maximum values of overall proportions (p1, p2) ranged from 0 to 1, and for discordant proportions (p12, p21) ranged from 0 to .9.
Tests of the difference between two discordant proportions produce the same outcome regardless of which proportion is assigned to p12 or p21, so to get the best estimate of the value to use for sample size estimation, we also analyzed the mean of the discordant proportions from each study. As expected from our analysis of the sample size formula, the maximum and minimum means of discordant proportions ranged from .01 to .50 (the theoretical maximum range is from 0 to .50).
The primary goal of these analyses was to find good estimates for the magnitude of discordant proportions to use in sample size tables for within-subjects comparison of dependent proportions. Following the strategy we used for rating scales, we provided sample size estimates for the center of the distribution as the typical value (.22 whether measured with the mean or median) and for a slightly more conservative but realistic value of .28 (the 75th percentile, upper limit of the interquartile range).
Sample Size Estimation Tables
Tables 3 (for 95% confidence) and 4 (for 90% confidence) show the sample size estimates for within-subjects studies that will include comparison of discordant proportions. Both tables show a range of effect sizes from 1% to 50%, sample sizes for effect sizes centered around the median estimate of discordant proportions (.22), sample sizes for effect sizes centered around the conservative realistic estimate of discordant proportions (.28), and sample sizes for between-subjects comparisons of independent proportions assuming maximum binary variance (p = .50) for two independent groups (for comparison with within-subjects sample sizes). The tables demonstrate the efficiency of the within-subjects design relative to between-subjects. For the typical value of discordant proportions (.22) and effect sizes 30% or smaller, the within-subjects sample sizes are about 44% of the between-subjects sample sizes. For the conservative estimate (.28) and effect sizes 30% or smaller, the within-subjects sample sizes are about 56% of those for between-subjects.
| Effect Size | Within Subjects (pdiscordant = .22) | Within Subjects (pdiscordant = .28) | Between Subjects (p = .50, two groups) |
|---|---|---|---|
| 50% | * | 22 | 26 |
| 40% | 25 | 27 | 44 |
| 30% | 38 | 47 | 82 |
| 20% | 84 | 107 | 190 |
| 15% | 151 | 192 | 342 |
| 12% | 237 | 302 | 540 |
| 10% | 343 | 436 | 780 |
| 9% | 424 | 539 | 964 |
| 8% | 537 | 683 | 1220 |
| 7% | 702 | 893 | 1596 |
| 6% | 957 | 1217 | 2174 |
| 5% | 1379 | 1754 | 3134 |
| 4% | 2156 | 2743 | 4900 |
| 3% | 3834 | 4880 | 8716 |
| 2% | 8631 | 10985 | 19616 |
| 1% | 34532 | 43950 | 78482 |
| Effect Size | Within Subjects (pdiscordant = .22) | Within Subjects (pdiscordant = .28) | Between Subjects (p =.50, two groups) |
|---|---|---|---|
| 50% | * | 17 | 20 |
| 40% | 20 | 21 | 34 |
| 30% | 30 | 37 | 64 |
| 20% | 67 | 84 | 150 |
| 15% | 119 | 151 | 270 |
| 12% | 187 | 238 | 426 |
| 10% | 270 | 343 | 614 |
| 9% | 334 | 425 | 760 |
| 8% | 423 | 538 | 962 |
| 7% | 553 | 704 | 1258 |
| 6% | 754 | 959 | 1714 |
| 5% | 1086 | 1382 | 2468 |
| 4% | 1698 | 2161 | 3860 |
| 3% | 3020 | 3844 | 6866 |
| 2% | 6799 | 8653 | 15452 |
| 1% | 27201 | 34619 | 61822 |
How to Compute a Sample Size Estimate
As an example of how the values in the tables were computed, here are the steps for Table 3 (95% confidence) when the effect size is 10% and pdiscordant = .28. Note that the value for z is 2.802, 1.96 (for 95% confidence) plus .842 (for 80% power). The values for p12 and p21 need to be determined such that p12 − p21 equals the effect size with .28 centered between the two discordant proportions. For this example, p12 is .33, and p21 is .23.
Before computing the sample size, we refine the values of p12, p21, and d to be consistent with the adjusted-Wald version of the confidence interval around the difference in dependent proportions. Referring to Table 1, the adjustment is to add z2/8 to cells a, b, c, and d and z2/2 to n, as shown in this three-step process.
Step 1: Compute initial value for n.
- n = z2(p12 + p21)/d2 − z2
- n = 2.8022(.33 + .23)/.12 − 2.8022
- n = 7.851(.56)/.01 − 7.851
- n = 432
- Rounded up: n = 432
Step 2: Adjust p12, p21, and d based on initial estimate of n.
- padj12 = (.33(432) + .9814)/(432 + 3.9256) = .3293
- padj21 = (.23(432) + .9814)/(432 + 3.9256) = .2302
- dadj = .3293 − .2302 = .098
Step 3: Compute the adjusted sample size.
- n = z2(padj12 + padj21)/dadj2 − 1.5z2
- n = 2.8022(.3293 + .2302)/.12 − 2.8022
- n = 7.851(.5595)/.0098 − 11.777
- n = 435.5
- Rounded up: n = 436
How to Use the Tables
To use the tables to estimate sample size requirements for within-subjects studies with dependent proportions:
- Determine whether you want confidence at the publication level (95%; Table 3) or the industrial level (90%; Table 4).
- Determine the smallest effect size for which you want to be able to claim statistical significance.
- Decide whether to use a typical (.22) or conservative (.28) estimate of the likely discordant proportion.
- Plan for the indicated sample size.
Here are a few examples.
Success rates for two online payment designs. Suppose you plan to conduct an unmoderated usability test of two online payment designs where the key outcome variable is a successful payment. You decide to reduce the risk of having more variability than expected, so you decide to use the 75th percentile estimate of discordant proportions (.28) and to test with 95% confidence and 80% power. You want to be able to declare significance when the difference is as small as 8%. For these requirements, you’ll need 683 participants.
- Confidence: 95% (Table 3)
- Power: 80%
- Estimated discordant proportion: .28
- Effect size: 8%
- Sample size: 683
Willingness to use two proposed home page designs. You’re running a quick screening study to see how users respond to the appearance of two home page designs by having them indicate for each design whether they would be willing to use it. You decide 90% confidence is sufficient, the typical value for discordant proportions is appropriate (.22), and at this stage of development, you’ll only reject a design if there is a difference of 30% or more in willingness to use. For these requirements, you’ll need 30 participants.
- Confidence: 90% (Table 4)
- Power: 80%
- Estimated discordant proportion: .22
- Effect size: 30%
- Sample size: 30
Quick Note on Discordant Proportions and Standard Deviations
You might have noticed that we didn’t specify a set standard deviation for the within-subjects sample sizes. Instead, we specified the magnitude of typical discordant proportions (median of .22, 75th percentile of .28). We did this because, when you vary the effect size around a set value for discordant proportions, the standard deviation varies along with the effect size. Specifically, the standard deviation is the square root of the sum of discordant proportions minus their squared difference (i.e., s = ((p12 + p21) – d2)½). Table 5 shows the standard deviations for the effect sizes and typical discordant proportions shown in Tables 3 and 4.
| Effect Size | pdiscordant = .22 | pdiscordant = .28 |
|---|---|---|
| 50% | 0.436 | 0.557 |
| 40% | 0.529 | 0.632 |
| 30% | 0.592 | 0.686 |
| 20% | 0.632 | 0.721 |
| 15% | 0.646 | 0.733 |
| 12% | 0.652 | 0.739 |
| 10% | 0.656 | 0.742 |
| 9% | 0.657 | 0.743 |
| 8% | 0.658 | 0.744 |
| 7% | 0.660 | 0.745 |
| 6% | 0.661 | 0.746 |
| 5% | 0.661 | 0.747 |
| 4% | 0.662 | 0.747 |
| 3% | 0.663 | 0.748 |
| 2% | 0.663 | 0.748 |
| 1% | 0.663 | 0.748 |
The lower value for discordant proportions (.22) has lower standard deviations, ranging from about .44 to .66, than the higher value (.28), which ranges from about .56 to .75.
Summary and Takeaways
What sample size do you need when comparing dependent proportions? You certainly need some standard types of information such as confidence, power, and the critical difference. When planning to compare dependent proportions with a McNemar Exact Test, however, you also need an estimate of the discordant proportions.
Sample size estimation for differences in dependent proportions is fundamentally different from estimation for independent proportions. For independent proportions, it is reasonable to assume p = .50 because that maximizes binomial variability and is a common outcome in practice (when p = .50, s = .50). Sample size estimation for differences in dependent proportions is trickier, but analysis of 50 real-world data sets indicates a typical value for discordant proportions of .22 and a conservative realistic (75th percentile) value of .28 that correspond to standard deviations ranging, for various effect sizes, from .44 to .75.
Sample size estimates for dependent proportions are consistently smaller than those for proportions from two independent groups. For the typical value of discordant proportions (.22) and effect sizes 30% or smaller, the within-subjects sample sizes are about 44% of the between-subjects sample sizes. For the conservative estimate (.28) and effect sizes 30% or smaller, the within-subjects sample sizes are about 56% of those for between-subjects. So, for a quick sample size estimate, you can use the sample size for a between-subjects table and cut the sample size in half (keeping in mind it is a rough approximation).
Where are the Goldilocks zones for dependent proportions? For many research studies, sample sizes as high as 500 are affordable, and effect sizes as high as 10% are sufficiently sensitive. For example, for discordant proportions of .22 in Table 4 (90% confidence, 80% power), the Goldilocks zone ranges from effect sizes of 10% to 7% with corresponding sample sizes from 270 to 553. You can adjust these sensitivity and attainability goals as needed for your research context.
